In the word of an engineer friend, proportional control is like working with a spring. For fellow physics enthusiast, F = -kx is a familiar expression that relates the force acting on an object attached to a spring (without damping) due to a displacement. The magnitude of the force increases (linearly) as the distance x increases. And k is the constant of proportionality that relates them.
Very similarly, we can use proportional control to change the behavior of our SciBorg (analogous to force) based on a change or error (analogous to displacement) recorded by a sensor.
In the third part of our SciBorg project, we related the speeds of the motors to a linear expression containing k*error to:
I) Driving Straighter Using Proportional Control
Very similarly, we can use proportional control to change the behavior of our SciBorg (analogous to force) based on a change or error (analogous to displacement) recorded by a sensor.
In the third part of our SciBorg project, we related the speeds of the motors to a linear expression containing k*error to:
I) Drive Straighter
II) Travel 10 ft and stop
III) Follow an object using an ultrasonoic sensor
IV) Follow a line using a light sensor
We set a base speed of 150 to both motors and changed the speed of Motor 1 based on the relation v1 = 150 + error * k, where error = encoder reading for motor 2 - encoder reading for motor 1, and k is an arbitrarily set constant of proportionality that we changed based on observations.
Below are the sketch used, the different k values tried and their serial port readings, as well as videos showing how the SciBorg performed on the lab floor, a carpet, when the wheels traveled on surfaces of different friction constants, and going up/down a ramp (we have yet to try because the ramp is not set up now).
Below are the sketch used, the different k values tried and their serial port readings, as well as videos showing how the SciBorg performed on the lab floor, a carpet, when the wheels traveled on surfaces of different friction constants, and going up/down a ramp (we have yet to try because the ramp is not set up now).
The results over several trials were fairly constant. The car looked less shaky than it did in the bang-bang control partly because proportional control results in gradual changes rather than abrupt turns.

 |
| K=0.1 |
 |
| K=0.3 |
 |
| K=0.5 On the lab floor: |
On a carpet:
With wheels on different surfaces:
Notice that the wheel on the smoother surface always moves faster and the car turns to the side away from this smooth surface. This is because we calibrated our k and our motor speeds for a surface where both wheels face the same amount of friction.
II) Go 10 feet
We used a similar logic of making the speed linearly dependent on some changing variable. But this time, we made the speed dependent on the number of encoder readings the car needs to go before it reaches its destination. This number of counts left decreases as the car approaches its destination, so it slows down before it finally stops.
First, we attempted to find the encoder reading after the car has traveled 10 ft by timing the car travel the 10 ft and then timing the encoder reading as it is attached to the serial monitor. Later, we figured where we recorded encoder values and where we ran the car are different environments in which friction and power supplied to motors varies (the computer actually provides additional energy to the motors).
Instead, we decided to calculate the number of encoder counts per rotation, which should be a constant value because the encoder readings come from physical structures within the motor.
We conducted the following mini experiment, where we took the ratio of the wheels' circumference to 10 ft and the encoder readings per turn to find the encoder readings per rotation.
(I will provide a more organized version of this picture with more time.)
Below are the sketch used and the video of Daniela (our SciBorg) stopping after traveling ~10 ft on the lab floor.
Notice the tail not the front of the car was on the start line and it stops very close to 10 ft from where it starts (less than 3 in of uncertainty). However, we also attempted to use the nudge function.
Sketches and video below:
Ideally, we would have used a relation that looks like speed = k * counts left. However, when the speed is really small, the car starts wobbling and changing direction. It also stops before speed is actually equal to zero. So the function of our proportional control ended up being mostly slowing the car down before we tell the motors to stop.
III) Using ultrasonic sensor follow objects
In this section we made the speed of the motors dependent on the distance of an object from the ultrasonic sensor. Given the relation, speed = 170 + k*error, the speed increases with a positive error and decreases with a negative error.
Again, because lower speeds result in an unstable SciBorg, we used the proportional control as a means of slowing the car down before it stops.

This worked well as the Daniela followed my feet and then other SciBorgs. I would say this worked as well as the bang-bang control method, especially because the stopping distance not precise as long as the SciBorg followed others and stopped before crashing into the object.
In this last video, Daniela was the one at the back.
In this section we made the speed of the motors dependent on the distance of an object from the ultrasonic sensor. Given the relation, speed = 170 + k*error, the speed increases with a positive error and decreases with a negative error.
Again, because lower speeds result in an unstable SciBorg, we used the proportional control as a means of slowing the car down before it stops.

This worked well as the Daniela followed my feet and then other SciBorgs. I would say this worked as well as the bang-bang control method, especially because the stopping distance not precise as long as the SciBorg followed others and stopped before crashing into the object.
In this last video, Daniela was the one at the back.
IV) Proportional line following
We faced the most challenge in this one because, while the logic made sense, the result was completely unpredictable.
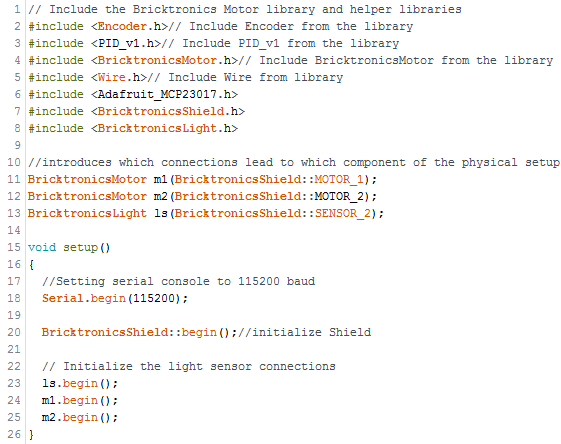
Our setup:
We placed the sensor to the left of the line and told the code to set speed of motor 1 to 150 + k*error, where error = value of brightness - 80. We took 80 because it was the reading right between the brown and the white surfaces.
With error > 0 speed of motor 1 should increase, therefore car turns towards motor 2; error < 0 speed of motor 1 should decrease, therefore car turns towards motor 1.
In practice, this didn't happen.
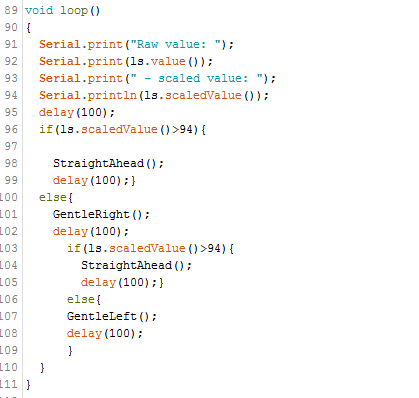
Here are some of the several loop commands we attempted:
In some of these cases the car just went straight ahead, while in others it just turned to the right.
Expect to hear back from me on this one.
Our setup:
We placed the sensor to the left of the line and told the code to set speed of motor 1 to 150 + k*error, where error = value of brightness - 80. We took 80 because it was the reading right between the brown and the white surfaces.
With error > 0 speed of motor 1 should increase, therefore car turns towards motor 2; error < 0 speed of motor 1 should decrease, therefore car turns towards motor 1.
In practice, this didn't happen.
Here are some of the several loop commands we attempted:
And when this didn't work:
In some of these cases the car just went straight ahead, while in others it just turned to the right.
Expect to hear back from me on this one.