Child Study Center Final Project: Week 4

This week, we tried our music shield, our lights, and our servo separately and then attempted to run them simultaneously. While each component worked individually, the combination failed. We figured later that this was because the music maker shield was using the pin we attempted to use for our servo. This means that we either had to use two separate Arduino micro controllers (1 for music only and another for LEDs and a servo motor) or that we had to be extra careful about which pins we used if we were to keep using the same Arduino for all our outputs. Before we hit this hurdle, however, there were a few accomplishments and mini failures we went through.


Soldering the music maker shield:
Because our music maker shield came in pieces, we had to solder the parts according to Adafruit's online instructions. Since solder includes lead, we were careful not to breath in the fume and used a fume extractor whenever we soldered.

We then inserted an SD card with two files of music carefully named to match the format in the code. We had named them incorrectly before this to find that the music doesn't play unless it is named "Tracknnn" where is an integer 0-9. We also needed exactly 8 characters in our name. We connected a headphone to the black port and ran the following code:

The songs played while the serial monitor showed "played." When the music stopped playing, the monitor printed "done playing." Since this worked well, we tried connecting our speaker to the blue ports and ran the code again. While the music played and the serial monitor showed the appropriate status reports, the volume was really low. Circled in the code above is a part that controls the volume. As it is the volume is set to (20,20) and it says that the lower these numbers, the higher the volume. So we ran the code over and over with much lower numbers but still couldn't adjust the volume. 
                                    

We asked for Amy's help at this point and moved on to work on the servo and LEDs.

Servo and LEDs in one:
We used the following code to operate the servo and LEDs together. Because we defined PreviousMillis (the total time that has passed since the program started running) as an integer and not as an unsigned long, we had problems on the second or third rounds of running the system. The value of previousMillis would get stuck and give us only one LED lighting up instead of the expected pattern.

We also had a hard time making the servo stop after a certain amount of time. As we tried to troubleshoot the servo's tendency to never stop running, we learned that we were using a continuous servo motor that keeps increasing its angle with each round. Even as it oscillates back and forth, its net position shifts. This is not ideal for a movement we plan to resemble that of human wrists, because wrists don't keep on rotating infinitely. Once we switched our servo motor to the correct type, we still noticed that the command that tells it to go to a specific position and stay didn't work. Part of our goal for the next week is to work on controlling the servo better.

Lastly, our music maker stopped working after we connected it to our servo. It started reading "done playing music" even when it obviously didn't and we couldn't hear anything from the speakers. This may mean we have erased some data regarding the pins the music maker shield needs to use in order to play music. This could involve adjusting parts of the library and may take lots of time (unrealistic to our timeline), but we have our fingers crossed.

CSC Final Project Week 3

This week, we ordered our materials, identified those available in the lab for us, and started making prototypes. 

The materials we ordered were:

i) A "music maker" shield, an SD card, and a 0.5 W speaker

ii) A sheet of Velostat 

Ordered Materials

i) A music maker shield

Since we wanted music to entertain the children while encouraging them to wash their hands properly, we searched for shields compatible with Arduino Uno that can play recorded music. We found "Adafruit 'Music Maker' MP3 Shield for Arduino w/3W Stereo Amp - v1.0" (shown in the images below) that can take an SD card and play different tracks of music saved in mp3 format. We also ordered the SD that would go with the music maker.

To go with our music maker, we also ordered an 8 Ohm, 0.5 Watts speaker thinking the low power would save us battery life.

Although this speaker looked tiny and exposed (without a case), we believed it was appropriate for a project of our scale and budget. We also planned to either build a container for it or mount it higher up to prevent children from splashing water on it. 

ii) An 11'' by 11'' Pressure-Sensitive Conductive Sheet/Velostat

We had originally planned to use a force sensor (force plate) that reads the weight of the person standing on it and allow us to only activate the actuator if a child (under a certain weight) stands on it. However, we couldn't find any force plates within our budget and of the appropriate size.

First, we settled for a button under a hard lamina that would push the button as a person stands on it. But since this would involve building a platform that is both stable and effective in pushing the button even if the child stands slightly beside the button, we went with Amy's suggestion of a Velostat. 

A velostat is a sheet of material whose electric resistance decreases when pinched. This allows us to put conductive wires on either side of the sheet and have the sheet act as a poor conductor when relaxed and a better conductor (low resistance) when stood on. This, if it works, would be a cheap and convenient input method for our design. 

This is what a sheet of Velostat looks like

Early Prototyping

We started our prototype by reviewing and building on some of the Arduino exercises we had done before. 

We built on the "Blink" example from the Arduino program to control first one and then multiple LEDs. This prepared us to to set up the LEDs that would shine at specific times behind each instructional picture to help students focus on the appropriate step of hand washing at a given time. 

We also revisited our "Sweep" example with servos and adjusted the angles of rotation of the servo motors to resemble a more realistic wrist rotation. We cut out cardboard and foam board models of tiny hands (almost real-life-sized models of a child's hands) and taped them to the servo to simulate moving hands, which when put next to each other look like they're washing. 

First, we had attached a servo to each hand and oriented the hands such that they face perpendicular to the wall. Later, Amy suggested we use a servo on one hand and keep the other stationary. That way, we can orient the hands better for visibility, and minimize power consumption by only using one servo. The relative motion between the hands would still make them look like they are scrubbing/washing.

Overall, this week was spent ordering and trying components of our design for functionality. We were also able to solder parts of our music maker shield in preparation to use it the next week. 

CSC Final Project: Week 2

This week, we visited the Child Study Center again to observe the children washing their hands and introduce our plan to Becky, the director of the center. While we got some constructive comment from Becky on our rough proposal, we couldn't observe the children washing their hands due to a temporary problem with the tap water. 

The importance of customer feedback/suggestions and adapting our model to the existing setup

As a reminder, our original idea was to help 2 to 4 year olds wash their hands more effectively and for long enough by building a feedback control system that would detect the weight of a child in front of the sink and activates three outputs:

i) a voice that encourages them to wash their hands followed by a shong about washing hands

ii) a row of LEDs that resemble the "loading..." bar and signal the passage of time

iii) Small cutouts of hands attached to servos that move back and forth resembling the motion of washing hands. 

Becky told us that the idea sounds doable but added a few tips to better serve the center's needs and interests. Here are some of the features she recommended:

i) A way to either shut off or reduce volume for "quiet times" in the building

We plan to build a potentiometer into our system to give the teachers at the center this control.

ii) To incorporate pictures (like they have in front of the sinks at the center) into the "loading..." LEDs. This is important because the children tend to forget the visual cue exists after they get used to it and they need something to draw their attention. 

We plan to enlarge their visual cues (figure 1) and orient the LEDs such that each LED stands above or behind a cartoon that describes a certain procedure and lights up only when it is time for the child to be that particular stage of washing their hands.

Figure 1: Existing visual cue at the center

iii) To make the weight sensor or button we would use to sense the presence of a child in front of the sink flexible to sit on a stool or on the ground. Some kids are shorter than others and need to stand on a stool to reach the sink. By either building two buttons as sensors (one on the stool one on the floor) or by building one that can be moved to either level, we will serve children of all heights.

Figure 2: Stools for shorter children at the center

We incorporated these tips to our plan before we formally presented our idea to the client on Friday, April 8th. 

MATLAB: Thermal Systems Part 2

In this section we applied our experience with the first part of our thermal systems lesson to a real thermal system. We used a serial port to pass information between our MATLAB code and a circuit with a heater and a temperature sensor. 

Objectives:
1) Simulate temperature vs time graphs and compare them to the data from the heater
2) Calculate values of Rth and C such that our temperature approaches 340 K within 300 seconds
3) Modify our code into a bang-bang control and compare the simulation to data
4) Modify our code into a proportional control and compare the simulation with data

1) Simulating the temperature vs time graph

We ran the given heatsim.m script:

Once we wrote these separate codes, we thought it would be easier to compare the graphs if they were on the same axes and wrote the following to "unite" them:

Data from heater

Comparing simulation with data from heater

As you can see from the graph, the simulation fits the experimental data well but not perfectly. Perhaps, with more time, the curves may have deviated from each other more.

 2) Calculating values of Rth (resistance) and C (heat capacity) such that our temperature approaches 340 K within 300 second:

We used the relations: Rth = deltaT/P and C = Power/(delT/dt) from the last part of thermal systems to find C and Rth. We found Rth = 34.076 K / 6.5W = 5.24 K/W, and C = 6.5 W / (0.33022 K/s) = 19.68 J/K.

It is these values we used to simulate the above red curve.

C and Rth are related by τ = Rth*C, where τ is the time it takes for a system to reach ~63.2% of its final asymptotic value. To find τ we took 63.2% of the difference between the maximum and minimum temperature of the system recorded. This value was only 10 units away from the value we found by multiplying the thermal resistance and heat capacity. That means the experimental data and the model used for simulation match up reasonably well.

3) Bang-bang control simulation and experimental data
We modified our heatsim.m script to include a for loop that creates a vector and made the power supplied dependent on whether or not the temperature read reaches 340 K. If the desired temperature is reached or surpassed we set power to zero, else we set it to 100% of its maximum value.

This yielded the following simulation graph:

For the experimental part of our bang-bang control objective, we modified the "test thermal" script to included a similar if/else statement to turn power on or off depending on temperature readings. 

This yielded the following experimental data:

While the simulation and the experimental graph both level off and oscillate with a very small amplitude at T ~ 340 K, the experimental curve reaches the temperature much faster. This could be because our C and Rth values were from a different day and possibly different heater. Ideally, we would use controlled conditions to make the simulation match the experiment perfectly.

4) Proportional control simulation and data:
Here, we made power supplied to the heater linearly dependent on the error (how far the current reading is from the desired value). The larger the error, the more power the system we apply to make sure the "coffee" heats up fast at the beginning, when it is cooler, but the rate of change of temperature slows down as the temperature approaches 340 K. We tried this with three values of K: 0.05, 0.2, and 0.5. While 0.5 gave the closest value of temperature to 340 K within the 300 seconds limit, it was still significantly lower than we wished. So, we optimized our parameters to reach 340 K faster. We changed the power expression to 5 + error*K to boost up the power but limited the upper bound to 6.5 so it never exceeds the maximum power the heater can supply. This worked better and gave us a graph with 340 K as an asymptotic value.

Here are the sketches and simulations:

K = 0.05

K = 0.2

When we set P = 5 + error*k, in the form power = constant + error * (proportionality constant), the graphs approach 340 K much better. This is safe because we still restrict power from exceeding 6.5 W, the maximum value, and it gets the task done better.

K = 0.5

K = 0.2

Notice, in both cases, the larger K values work better in terms of reaching 340 K.

We then modified our "test thermal" script again to incorporate proportional control. Since the power we defined was actually some percentage of the setpower command that actually communicates with the heater, we created a new variable called percentpower = power/6.5*100 and plugged it into the setpower command.

Here are the script and graph:

The proportional control simulation seem to model the experimental data curve better because the significant decrease in slope happens at around 100 seconds in both the simulations and in the experimental data. But (unsurprisingly) the experimental data looks a lot less smooth. I attribute this to the inconsistent ambient temperature and draft in the room.

My take on this:
As a physicist-to-be it bugs me a lot not being able to do this experiment under controlled conditions like the same day, with constant ambient temperature and using the same heater. However, we had to collect the first half of the data on one day and the rest on another and we had to switch between heaters while we waited for one to cool. This made the initial temperature inconsistent between different experiments. But on the bright side, we still managed to accomplish the goal of modeling and observing the experimental results of thermal systems with and without control systems.

Final Project with Child Study Center - Week 1

My partner, Thessaly, and I chose to work with the Wellesley Child Study Center for our final project. Before picking two possible projects, we considered a lot of the problems (or "things that could be better" as she phrased it) that the director of the center suggested we tackle. Some possible projects were a way to alert teachers when students want to climb up and down ladders, a fun and risky-feeling game that actually doesn't risk the children's safety, a way to make children aware of time, a system that reminds children to switch between games without adults having to repeatedly tell them, or a way to make children wash their hands thoroughly.


We chose to work with either a "clock" for children or a system that would make washing hands fun for children and make them follow the right steps when cleaning their hands.

1) A "heart timer"

As we tried to show in the first slide of our presentation to our class, we proposed making a heart-shaped assortment of LEDs that light up in pattern that makes it look like the heart is growing as time passes by. We chose the heart shape to symbolize affection and the proximity of someone dear to the children coming soon (their parents coming to take them home at the end of the day). Since the time for activities or for the entire day varies, we planned to make the range adjustable using a potentiometer (for continuous times) or a set of buttons each representing an amount of time to set the "timer" to.

We later discussed this with Amy, our professor, and realized that the heart shape may be too abstract for the 2-4 year-old children, and that the growth of the size may not be very noticeable.


2) An interactive sink

Our second idea was a feedback-control system that would engage and inform children as they wash their hands to make sure they do so for the appropriate amount of time and following the right steps. This tackles the problem that a lot of the children at the center either completely forget to wash their hands, do without soap, or don't spend enough time to do so.

Here, we planned to place a force sensor under the sink where the child would stand and an ultrasonic or motion sensor next to the sink where it can sense the child's hands under the faucet. We planned to have the force sensor trigger a voice that welcomes the child, invites them to start washing their hands, and promises to start singing if they start washing their hands. The ultrasonic sensor, when detecting hands under the faucet would trigger a song about washing hands. This lasts 20 seconds, the recommended amount of time for a child to be washing their hands. The voice, controlled by Arduino  would then cheer and encourage the child to close the tap, dry their hands and go.

As a mechanical component, we also included a pair of 3D hands to move (using servo motors) in a way that resembles hand washing movement to catch the child's attention and give a visual suggestion to wash their hands.

After our presentation and discussion with Amy, we considered incorporating the first idea into the second: we may be able to have an LED timer (looking more like the "loading..." bar that gives children a sense of time as they wash their hands.

At this point, we have no clue how to make music with Arduino or if any of this will work out as planned, but we are really excited to work on our very own project and for a real client. Expect more about our final project in the coming weeks.


Thanks for your time.

Meba

MATLAB: Thermal Systems Part 1

On Friday April 1st, we used MATLAB to model the heating and cooling of a cup of coffee under different conditions. We took the following expression that gives the temperature of a system exposed to air as time passes.

where dT = a small change in temperature

C = heat capacity

T = Current temperature

Tair = Temperature of the surrounding air

Rth = Thermal resistance

dt = a small change in time

Question 1:

How does the cooling behavior change if we vary the parameters and C? Figure this out using intuition and the above equations, and then vary these parameters in your program to confirm your conclusions.

Rearranging the above equation, T = Tair - (dT/dt) *(RthC). T is proportional to Rth and C. Therefore, increasing Rth would increase T as would increasing C. But we can also see from this same equation that dT/dt is inversely proportional to Rth and C. So with larger Rth or larger C values the change gets steeper. And smaller Rth and C values give a curve with smaller slopes at different parts. 

To test this, we modified the following code as noted in the comments and got the following results:

C = 100; Rth = 0.85

C = 10000; Rth= 0.85
Here, the temperature has shifted upwards (as expected, since C*Rth increased). But the slope over each small time interval has significantly decreased.  

C = 1000; Rth = 0.085
Here, you can see that the graph resembles the C = 100; Rth = 0.85 graph. This shows that it is  really the product of C and Rth that affects the slope. 

We intentionally chose values of Rth and C dramatically different from the original values to see the change clearly. 

Question 2: Calculate a good value for P if we want our coffee to heat up to the Starbucks ideal 84°C, using the Rth from the MATLAB script?

This time, we considered a system where the coffee is sitting on a heating plate that provides a power of P. We used the following expression to find the value of P that would heat up the coffee to 84°C.

P = (dT/dt)C + (T-Tair)/Rth; where Rth = 0.85

But at t = 0, dT/dt = 0. So P = (T-Tair)/Rth = (84 - 20)/0.85 

P = 75 J/s

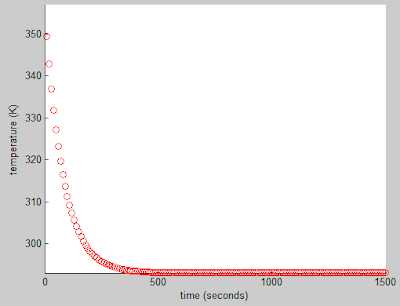
From the following graph deduce the thermal parameters C and Rth: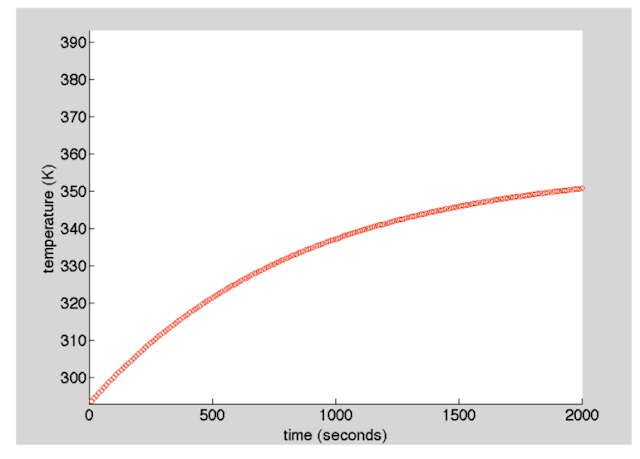

From the relation,  P = (change in T) / Rth, we can rearrange to get Rth = (change in T) / P, which in this case is about (350 - 290) K / 75 Watt = 0.8 K/Watt.

From dT/dt = P/C at t = 0, we can rearrange to get C = P/(dT/dt)

If you focus on the first part of the curve near t = 0, it resembles a line with a slope of 20/250 = 1/12.5

Therefore C = 75 W * 12.5 s/K = 937 J/K ~ 1000 J/K, which is the given value. My values are a little off because we can only make estimates from the graph.  

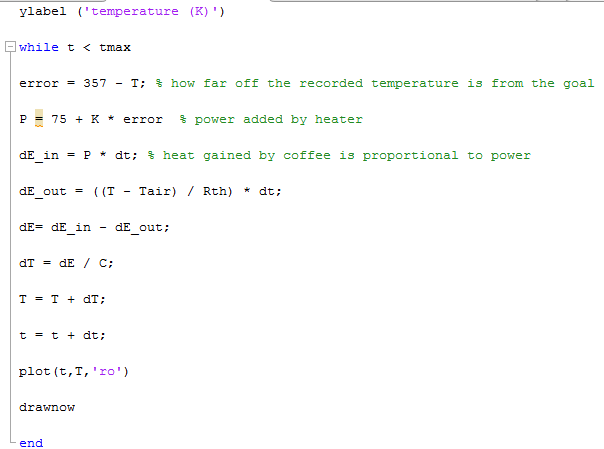
Question 3: Simulate a temperature controller that uses bang-bang control to reach and maintain the desired temperature. Bang-bang control is a very common approach for thermostats. 

We used the following script:

And we got the following graph:

After T = 357 the curve starts oscillating very subtly. This is because the power turns off when the temperature exceeds 357 K  and turns on when it drops below this desired value. Since it always overshoots the goal a little bit, some oscillation is expected but since the temperature stays very close to 357 K, the coffee will still be very close to the desired temperature, and certainly not much hotter or colder. 

Why is bang-bang control appropriate for many thermal systems? When might it be insufficient?

Thermal systems like this one can be adjusted to a good enough precision to maintain a certain temperature. The small fluctuations in temperature as the system continuously adjusts its output keep systems like thermostats at reasonably close temperatures to the desired value. This might be insufficient if a very precise constant temperature is desired or if one needs a continuous and shift in temperature as a reaction to a drop or increase in the measured. 

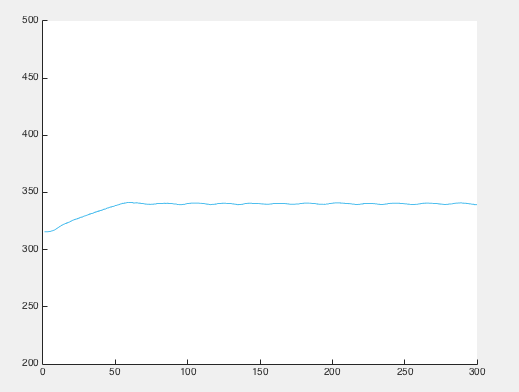
Question 4: Create a program that uses proportional control to reach and maintain the desired temperature. How does this approach compare to bang-bang control?

We used the following script:

 And we obtained this graph:

This graph appears a lot smoother and the value of the final temperature constantly approaches 357 instead of oscillating between values slightly above and below this point (unlike bang-bang control). This is because the power supplied to the coffee decreases linearly as the temperature approaches the goal. So, we prevent overshooting the goal and having to come back for it. 

This gives a more steady and precise temperature. It is also easier to reach the desired temperature in a short amount of time. 

Question 5) Suppose there is a delay between the time the coffee reaches a given

temperature and when the temperature sensor records that temperature. Modify

both of your programs to include this effect, along the lines of the programs on the next few pages that I showed in class, which explore the effect of adding a “sensor delay” to a simulation of moving a SciBorg lego car a particular distance. 

Here are the bang-bang and proportional control codes respectively that account for the delay (chosen to be 5 seconds here).

Bang-Bang Control with delay:

Proportional control with delay:

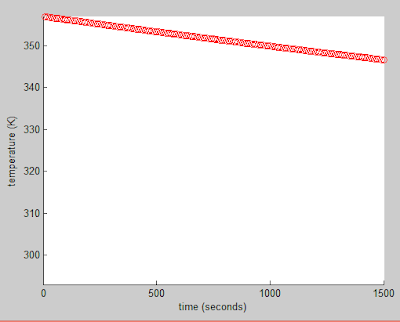
This yielded: 

Proportional control with a delay of 5

This graph shows a brief oscillation before it flattens at around 355.

What other might you expect in your thermodynamic system, apart from sensor delays?
I would expect a delay in heat transfer. Since radiation goes at the speed of light and everything else at a lower speed, there is always a time lag between heat loss or gain by the coffee.
In addition, the actuator itself would have a lag between it receives the "order" to turn on the power supply and when it actually does.