MATLAB: Thermal Systems Part 2

In this section we applied our experience with the first part of our thermal systems lesson to a real thermal system. We used a serial port to pass information between our MATLAB code and a circuit with a heater and a temperature sensor. 

Objectives:
1) Simulate temperature vs time graphs and compare them to the data from the heater
2) Calculate values of Rth and C such that our temperature approaches 340 K within 300 seconds
3) Modify our code into a bang-bang control and compare the simulation to data
4) Modify our code into a proportional control and compare the simulation with data

1) Simulating the temperature vs time graph

We ran the given heatsim.m script:

Once we wrote these separate codes, we thought it would be easier to compare the graphs if they were on the same axes and wrote the following to "unite" them:

Data from heater

Comparing simulation with data from heater

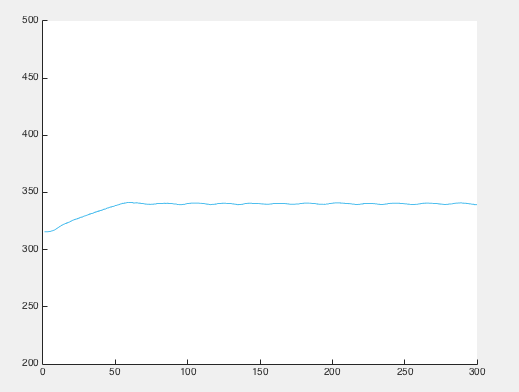
As you can see from the graph, the simulation fits the experimental data well but not perfectly. Perhaps, with more time, the curves may have deviated from each other more.

 2) Calculating values of Rth (resistance) and C (heat capacity) such that our temperature approaches 340 K within 300 second:

We used the relations: Rth = deltaT/P and C = Power/(delT/dt) from the last part of thermal systems to find C and Rth. We found Rth = 34.076 K / 6.5W = 5.24 K/W, and C = 6.5 W / (0.33022 K/s) = 19.68 J/K.

It is these values we used to simulate the above red curve.

C and Rth are related by τ = Rth*C, where τ is the time it takes for a system to reach ~63.2% of its final asymptotic value. To find τ we took 63.2% of the difference between the maximum and minimum temperature of the system recorded. This value was only 10 units away from the value we found by multiplying the thermal resistance and heat capacity. That means the experimental data and the model used for simulation match up reasonably well.

3) Bang-bang control simulation and experimental data
We modified our heatsim.m script to include a for loop that creates a vector and made the power supplied dependent on whether or not the temperature read reaches 340 K. If the desired temperature is reached or surpassed we set power to zero, else we set it to 100% of its maximum value.

This yielded the following simulation graph:

For the experimental part of our bang-bang control objective, we modified the "test thermal" script to included a similar if/else statement to turn power on or off depending on temperature readings. 

This yielded the following experimental data:

While the simulation and the experimental graph both level off and oscillate with a very small amplitude at T ~ 340 K, the experimental curve reaches the temperature much faster. This could be because our C and Rth values were from a different day and possibly different heater. Ideally, we would use controlled conditions to make the simulation match the experiment perfectly.

4) Proportional control simulation and data:
Here, we made power supplied to the heater linearly dependent on the error (how far the current reading is from the desired value). The larger the error, the more power the system we apply to make sure the "coffee" heats up fast at the beginning, when it is cooler, but the rate of change of temperature slows down as the temperature approaches 340 K. We tried this with three values of K: 0.05, 0.2, and 0.5. While 0.5 gave the closest value of temperature to 340 K within the 300 seconds limit, it was still significantly lower than we wished. So, we optimized our parameters to reach 340 K faster. We changed the power expression to 5 + error*K to boost up the power but limited the upper bound to 6.5 so it never exceeds the maximum power the heater can supply. This worked better and gave us a graph with 340 K as an asymptotic value.

Here are the sketches and simulations:

K = 0.05

K = 0.2

When we set P = 5 + error*k, in the form power = constant + error * (proportionality constant), the graphs approach 340 K much better. This is safe because we still restrict power from exceeding 6.5 W, the maximum value, and it gets the task done better.

K = 0.5

K = 0.2

Notice, in both cases, the larger K values work better in terms of reaching 340 K.

We then modified our "test thermal" script again to incorporate proportional control. Since the power we defined was actually some percentage of the setpower command that actually communicates with the heater, we created a new variable called percentpower = power/6.5*100 and plugged it into the setpower command.

Here are the script and graph:

The proportional control simulation seem to model the experimental data curve better because the significant decrease in slope happens at around 100 seconds in both the simulations and in the experimental data. But (unsurprisingly) the experimental data looks a lot less smooth. I attribute this to the inconsistent ambient temperature and draft in the room.

My take on this:
As a physicist-to-be it bugs me a lot not being able to do this experiment under controlled conditions like the same day, with constant ambient temperature and using the same heater. However, we had to collect the first half of the data on one day and the rest on another and we had to switch between heaters while we waited for one to cool. This made the initial temperature inconsistent between different experiments. But on the bright side, we still managed to accomplish the goal of modeling and observing the experimental results of thermal systems with and without control systems.